M. Garreau (a,b), R. Moreno (c,d), T. Puiseux (b,d), S. Toupin (e), D. Giese (f),S. Mendez (a), and F. Nicoud (a).
a : IMAG, Univ. Montpellier, CNRS, Montpellier, France; : b Spin Up, ALARA Group, Strasbourg, France; c : ALARA Expertise, ALARA Group, Strasbourg, France; d : I2MC, INSERM/UPS UMR 1297,Toulouse, France; e : Siemens Healthcare France, Saint-Denis, France; f : Magnetic Resonance, Siemens Healthcare GmbH, Erlangen, Germany
4D Flow Magnetic Resonance Imaging (MRI) is an imaging technique, which allows to quantify blood flow dynamics inside a 3D volume over the cardiac cycle (Markl et al. 2003). It has gained interest over the recent years, yet its clinical use remains limited due to itslow spatio-temporal resolution and various potential sources of errors: imaging artifacts, complexities inherent to the MRI acquisition procedure… To numerically simulate the MRI process could be an interesting way to investigate and decompose errors related to hardware issues from errors originating from the acquisition process itself. Another modality to predict hemodynamics is Computational Fluid Dynamics (CFD), which could be coupled with MR physics. The present study proposes a CFD-MRI simulation framework, where Navier-Stokes and Bloch equations are solved simultaneously in an Eulerian-Lagrangian formalism (Puiseux et al. 2021). An application is presented on a rigid flow phantom, whose geometry produces complex flow patterns as can be observed in the cardiovascular system.
Fig. 1 presents the geometry and the pulsatile inflow, which comes from in-vitro experimental 4D flow MRI data based on the same phantom (Garreau et al. 2022). Besides the mesh and boundary conditions, the MR pulse sequence is another input into our simulation, corresponding to the chronogram of the external magnetic field. The MR sequences used in this work are based on a constructor sequence (WIP 4D Flow Siemens). The CFD tetrahedral-based mesh (2mm characteristic size) is seeded with Lagrangian particles (8/cell), which are massless tracers carrying a magnetization vector that evolves with their position and the effective magnetic field they experience. The first step of our solver is to compute the CFD velocity field. This velocity field is then interpolated on the position of particles. Bloch equations are solved for each fluid particle according to the current magnetic events. At particular time instants specified in the sequence, the global magnetization is computed and collected in the so-called k-space, which can be interpreted as the 3D Fourier transform of the image. The synthetic images (SMRI) are then reconstructed from k-space with in-house Python scripts.
Figure 1 (1) Geometry and MRI field-of-view (FOV). (2) Inflow – Lines indicate time instants for Fig. 2.
In the present work, two 4D flow MRI sequences are compared, a conventional one and another using partial echo (PE). PE consists in acquiring only a fraction of the k-space, relying on its symmetric properties. Here, the first 25% of the k-space is not acquired for the 2nd sequence. Whereas sequences can be designed so that position- and velocity-encoding occur simultaneously along two directions (here X and Y), there is an inevitable time delay between the velocity and spatial encoding along the last direction (here Z), as the latest has to occur during signal collection around the echo time TE. This delay, called displacement time TD, is known to be related with common misregistration artifacts(Steinman et al. 1997). More than reducing the acquisition time, PE allows to reduce TD. In the present work, the acquisition time has been kept equal for both sequences. TE is reduced from 4.20 to 4.16 ms, but TD decreases from 1.99 to 1.52 ms. Other sequence parameters are equivalent in both simulations. The images of the 2nd simulation are reconstructed according to the zero-filling method (Dyverfeldt et al. 2015).
Reconstructed velocity maps are obtained for SMRI and compared with phase-averaged CFD velocity fields, downsampled to the MRI spatial resolution (2mm isotropic). Qualitatively, good agreement is found between SMRI and CFD, where the main flow structures are preserved in all directions and for all cardiac phases, as illustrated in Fig. 2. Errors maps are computed based on the Root-Mean Square Error:
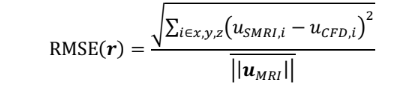
where u = (ux,uy,uz) is the velocity vector associated to the voxel at the position r, and uMRI is the in-vitro experimental time-averaged bulk velocity at the inlet used for normalization.
Figure 2 Velocity field and RMSE maps for the cardiac cycle instants (A) and (B) in Fig. 1.
In Fig. 2A, errors are found under the jetting flow after the junction between the collateral tube and the descending main pipe. The associated recirculation could account for the discrepancy. In the decelerating phase (Fig. 2B), the errors are mainly located in the collateral branch. The change of sign of ux in this narrow section could explain the misregistration of the SMRI velocity. The RMSE averaged over the cardiac cycle is of 0.28 for conventional SMRI and 0.24 for PE. As reference, the averaged RMSE computed for the matching conventional experimental MRI was found to be around 0.25 (Garreau et al. 2022). Thereby even though less signal is collected for the PE sequence, the shortened TD seems to improve the quality of the reconstructed SMRI velocity fields.
A numerical CFD-MRI solver is presented. The effect of the MR sequence parameter TD in the context of partial echo is investigated in a flow phantom with pulsatile inflow. In the present setup, to have a short TD despite less k-space data collected seems to improve the reconstructed velocity fields. Some perspectives are to impose an inflow closer to physiological conditions, to study different geometries (e.g stenosis to investigate acceleration-induced artifacts) and to implement additional sources of artifacts such as gradient non-linearities.
Acknowledgements
Simulations with YALES2BIO were performed using HPC resources from GENCI-CINES (grant numbers A0080307194 and A0100307194) and with the support of the MESO@LR-Platform at the University of Montpellier.
References
Dyverfeldt P, Bissell M, Barker AJ, Bolger AF, Carlhäll C-J, Ebbers T, Francios CJ, Frydrychowicz A, Geiger J, Giese D, et al. 2015. 4D flow cardiovascular magnetic resonance consensus statement. J Cardiovasc Magn Reson. 17(1):72.
Garreau M, Puiseux T, Toupin S, Giese D, Mendez S, Nicoud F, Moreno R. 2022. Accelerated sequences of 4D flow MRI using GRAPPA and compressed sensing: A comparison against conventional MRI and computational fluid dynamics. Magnetic Resonance in Med.:mrm.29404.
Markl M, Chan FP, Alley MT, Wedding KL, Draney MT, Elkins CJ, Parker DW, Wicker R, Taylor CA, Herfkens RJ, Pelc NJ. 2003. Time-resolved three dimensional phase-contrast MRI. J Magn Reson Imaging. 17(4):499–506.
Puiseux T, Sewonu A, Moreno R, Mendez S, Nicoud F. 2021. Numerical simulation of time-resolved 3D phase-contrast magnetic resonance imaging. Borazjani I, editor. PLoS ONE. 16(3):e0248816.
Steinman DA, Ethier CR, Rutt BK. 1997. Combined analysis of spatial and velocity displacement artifacts in phase contrast measurements of complex flows. J Magn Reson Imaging. 7(2):339– 346.
Keywords: Computational Fluid Dynamics (CFD) ; Hemodynamics ; Magnetic Resonance Imaging (MRI)
Restez informé grâce à notre programme relationnel gratuit pour les professionnels du rayonnement.